Why Is There No B or E Sharp? Secrets Unveiled

This post contains affiliate links. We earn commissions if you purchase products from retailers after clicking on a link from our site. As an Amazon Associate, we earn from qualifying purchases.

Hey… wait a second! If you look at all the notes of a chromatic scale, you’ll see this: C, C#, D, D#, E, F, F#, G, G#, A, A#, B, C. Where is E or B Sharp? Or F and C flat for that matter?

There is no definitive reason why our current music notation system is designed as it is today with no B or E sharp, but one likely reason is due to the way western music notation evolved with only 7 different notes in a scale even though there are 12 total semitones. Therefore 7 does not evenly divide into 12, thus our current music notation.

That sounds pretty confusing–I’ll try and diagram this out so we can understand this as best as we can. I’ll be honest, I’m not a music history expert by any stretch so we’ll learn together.

7 Note Scale: The Culprit For the Case Of the Missing B and E Sharp.

If you want an excellent source to understand the history of how we got our current 7 note scale, make sure and check this blog post out from Drooble–it’s decently comprehensive.

Suffice it to say, that we didn’t always have our full chromatic 12 note scale from the beginning. When music was being refined and systemized, there was initially only 7 notes that made up all the notes in a scale before the notes started repeating themselves. In other words, all the notes we thought about looked like this:

1	2	3	4	5	6	7	8
C	D	E	F	G	A	B	C (repeating the first note of the scale)

So we found that we could subdivide music into 7 (uneven) intervals before the notes started to sound the same but higher (what we call an octave, today).

So, how does this answer the question? Well, I think a diagram is in order.

The Beginning Of the Confusion

So, when music was just beginning to be diagrammed and plotted like it is today with modern music notation, we had 7 notes to work with.

In order to help us visualize, let’s think of an octave (where the note sounds the same, but higher. Like from C4 to C5 in modern terms), like a river.

The banks of the river (the top and bottom of the diagram) are the top and bottom of the octave. And the intervals are the planks that cross the river.

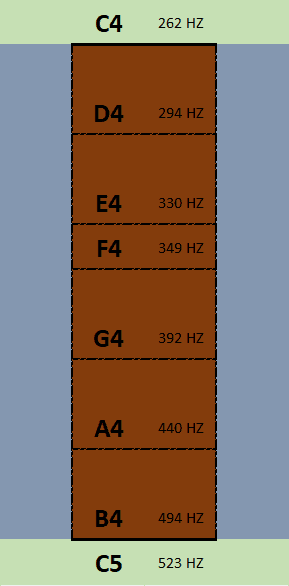
This is where the confusion started. Notice how the planks are uneven!

This unevenness is what gives the Major scale its distinct sound. The intervals go like this:

Full Step, Full Step, Half Step, Full Step, Full Step, Full Step, Half Step

Whether or not the first discovered notes made up a major scale are irrelevant, though, the point is that it’s extremely likely that the notes were not all the same logarithmic distance apart. See later in the article to hear why.

Whether it is known that the distance between each note was different at the time when they were “discovered” is unknown, but then, the cause of the weirdness of our music system came afterwards.

The Weirdness Starts

Fast forward to today’s musical notation, musician’s agreed that there were more than 7 notes between the banks of the river and eventually western musicians settled on 12 total notes in a scale.

The problem is that we didn’t redo the existing musical notation! Rather than starting from scratch and going from A to L (which we should have done in my opinion), we tried to meld the old system with the new.

So, instead of adding letters, we decided to add “sharps” and “flats”, as a way to describe the “semitones” between notes.

So, we have 12 total notes, making 12 intervals, which looks more like this:

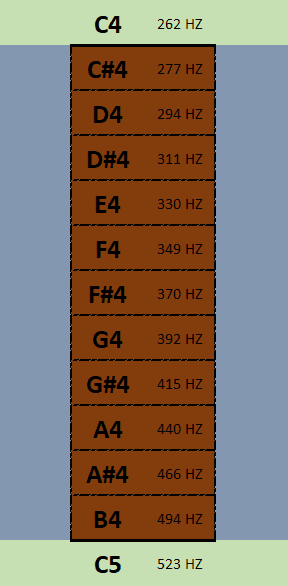
Notice how the planks in the 12 note bridge are all exactly even. They follow the same logarithmic ratio all the way up (2^(1/12)) the scale.

Now let’s compare these two bridges side by side:

Let’s take a look at the two bridges and pay attention to a few things:

• The starting and ending points are the same— in other words, the octave is the same distance in a 7 note scale vs a 12 note scale
• The C Major Scale Bridge (right) compared to the 12 note scale follows this pattern: 2 planks, 2 planks, 1 plank, 2 planks, 2 planks, 2 planks, 1 plank

So, back then, the musicians had a problem where they wanted to add 5 more notes to the original 7 note scale, but where to put them? There was no gap between E and F and B and C, but there was room for another note in between the rest of the notes.

Thus, a likely reason why we have no E# or B# today is because new music systems had to be designed to work with old music systems.

Is B Sharp the Same As C?

So, you may be wondering, if there is no B sharp, then why do you see it in music sometimes?

Well, the truth is that there is such a thing as a B# and an E#, it’s just that they are the same notes as C and F. That’s right, when you see sheet music that says B#, it will sound exactly the same as if you played a C.

In fact, the way we organize our current music depends on their being E#s and B#s, it’s all a part of how all of the notes interact together.

What makes far more sense is to not think of a sharp as one half-note higher, but instead one semitone.

A semitone is the distance of one interval in the 12 note scale. 12 notes = 12 semitones.

So, when a letter note has a sharp, like C, that means that C# is one semitone higher than C.

Conversely, a flat would be one semitone lower.

What’s the purpose of E# or B#? Why do we need multiple names for the same note?

The answer is all a part of the beautifulness of the circle of fifths. Check out Musical-U’s website for a super in-depth guide to the circle of fifths and how all the notes work together.

What E# Looks Like On a Piano

E# is the same as F.

To help you out, if you’re trying to find where the E# is on the piano, remember that E# is one semitone higher than an E. (On a piano, the next semitone is always the closest key, whether it’s black or white). If you look at the diagram above, you’ll see that is an F.

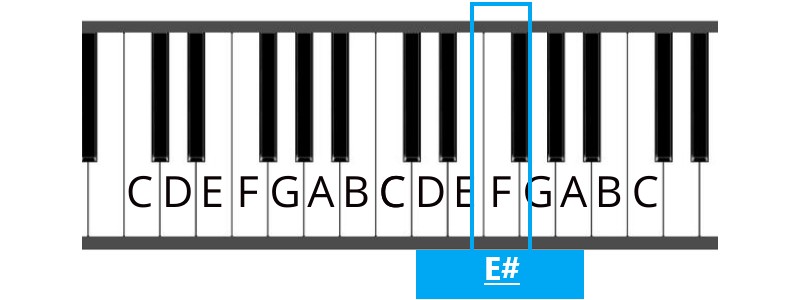
To close the gap, remember that since E# is F, that Fb is E.

What B# Looks Like On a Piano

B# is the same as C.

Remember now that B# is one semitone higher than B. Here’s the B# example

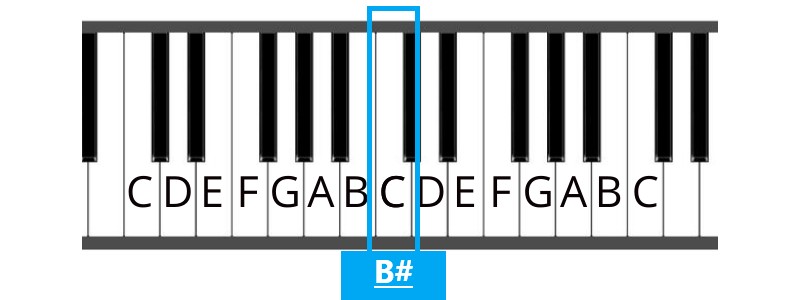
And then, remember that since B# is the same as C, that Cb is the same as B

What If The Original 7-Note Scale Had Equal Intervals?

So, back to our bridge analogy, what if the original 7-notes were the same (logarithmic) distance ( 2^(1/7)) apart? In other words, what would it sound like to have only 7 notes in a scale of equal temperament? (Check out Wikipedia for more detail on equal temperament)

In other words, what if the bridge looked like this:

To satisfy your curiosity (actually, probably mostly my curiosity), here is a sound clip of what it would sound like if all the notes were the same logarithmic distance apart:

The notes don’t really line up with the notes we are familiar with. But it sound interesting! Not exactly pleasing to the ear but definitely interesting.

It makes sense that back in the day without computers to help us how difficult it would be to figure this stuff out.

For reference, this is a C Major scale: